Flat-band systems, distinguished by their zero band dispersion, have emerged as a fascinating field of study due to their remarkable properties. These systems showcase localized eigenstates, a high density of states, and a remarkable sensitivity to interactions. This has spurred significant interest across multiple domains, including electronic, atomic, and photonic lattice systems. Traditionally, the pursuit of flat bands has been driven by the implementation of synthetic magnetic fields and the strategic use of destructive interference within lattice structures. These approaches, while effective, generally result in the formation of a limited number of flat bands; the majority of the bands retain their dispersive characteristics, including the edge states which are typically dispersive. The innovation of all-band-flat lattices marks a pivotal advancement in this arena. By meticulously engineering the hopping strengths among lattice sites, it is possible to achieve a lattice where every band is flat. This breakthrough allows for the comprehensive exploitation of all eigenstates and opens new avenues for exploring and manipulating the intricacies of flat-band physics. The full utilization of these eigenstates can potentially unlock new phenomena and applications in quantum simulations, materials science, and the development of novel electronic devices. 

Recently, the team led by Fei Gao from the College of Information Science and Electronic Engineering at Zhejiang University, in collaboration with the team led by Da-Wei Wang from the School of Physics, has realized an all-flat-band photonic lattice using microwave resonator array (Nat. Commun. 15, 1484 (2024)).

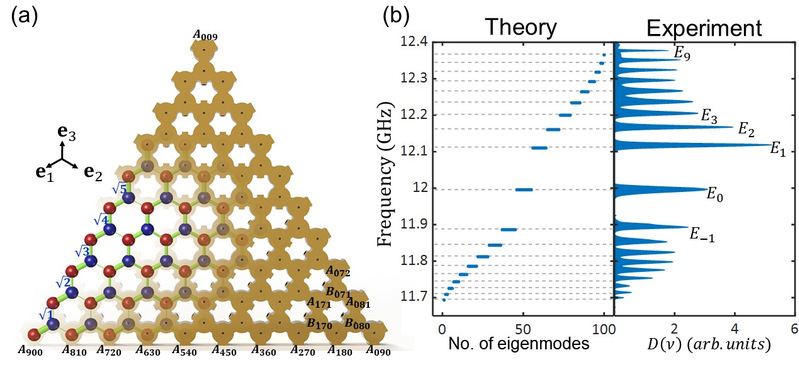
In this experiment, the research team precisely tuned the coupling strength of the microwave resonator array by adjusting the width of the waveguides. This approach was used to simulate two-dimensional Fock-state lattices, as described in the National Science Review (Vol. 8, nwaa196, 2021). The configuration emulated a honeycomb lattice, akin to strained graphene, and was achieved by coupling three cavities with atoms in the Fock-state space.  In this experiment, the coupling strengths between lattice sites were varied based on their positions, resulting in an energy spectrum characterized by a series of flat bands. Each site within the lattice was represented by a microwave cavity, with the inter-cavity coupling strengths carefully controlled. The all-flat-band energy spectrum was determined by analyzing the reflection spectra from these cavities. Furthermore, the experiment utilized an array of sources with varying phase differences to selectively excite different eigenstates, enabling precise manipulation and observation of the system's behavior. This approach has created a novel platform for exploring nonlinear physics phenomena within optical flat bands.